Chem 112, Exp 5: Determining Ka's Using pH Titration Curves

Experiment 5
Polyprotic Acids
Determining Ka's Using pH Titration Curves

Introduction:

pH Titration Curves 'Idealized':

To date the equivalence point of an acid base reaction has been determined using an indicator. In this experiment we are going to monitor the changes in pH that occurs during the titration of a weak polyprotic acid with a strong base. At the equivalence point one should expect to see a dramatic change in pH as the solution goes from acidic to strongly basic.
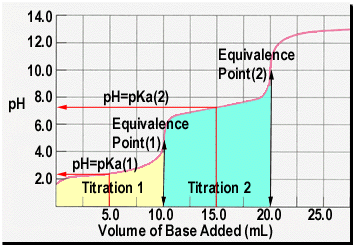Depicted on the left is an idealized pH titration curve for a weak diprotic acid. The first thing that you should notice is that there are two regions where we see a significant pH change. These, if you wish, correspond to two separate titrations. Titration 1 is the reaction of the first proton with the base (in this case sodium hydroxide).

H₂X(aq) + NaOH(aq) = NaHX(aq) + H₂O(l)

The second titration corresponding to the reaction of the second proton with sodium hydroxide

NaHX(aq) + NaOH(aq) = Na₂X(aq) + H₂O(l)

So, in essence, titrations of a weak polyprotic acid with a strong mono protic base are a combination of a number of titrations depending on the number of acidic protons on the polyprotic acid. The overall reaction is the sum of the two titration's

H₂X(aq) + 2 NaOH = Na₂X(aq) + 2 H₂O(l)

In determining the quantity of the acid or the molarity of the acid, we are normally just interested in the final equivalence point. In a pH titration plot, this is determined by finding the point of inflection on the final area where we see a significant rise in pH (This can be approximated by determining the midpoint.) However, this plot contains some other interesting features. First off, if we look at the area corresponding to the first titration, it should come as no surprise that its equivalence point corresponds to the addition of exactly 1/2 the volume of NaOH required to reach the final equivalence point. The real neat point comes at the 1/2 way point of each titration. Let us focus on the Titration 1. At the 1/2 way point, the concentration of H₂X(aq) remaining in the solution is equal to 1/2 the initial concentration of H₂X! The concentration of NaHX(aq) produced is also numerically equal to 1/2 the initial concentration of H₂X! So what, you may ask. Let's focus for a moment on the acid equilibrium associated with the acid that we are dealing with in titration 1.

H₂X(aq) + H₂O(l) ® HX^- + H₃O⁺
Ka = [H₃O⁺][HX^-]/[H₂X]

or written in another way

[H₃O⁺] = Ka{[H₂X]/[HX^-]}

using the concentrations that we know for H₂X and HX^- (=NaHX) at the 1/2 way point we get

[H₃O⁺] = Ka{1/2[H₂X]_initial/[1/2H₂X]_initial}
[H₃O⁺] = Ka

From the graph we can determine the pH at this point and since pH=-log10[H₃O⁺], we can determine [H₃O⁺] at this point and thus obtain the Ka for this equilibrium. Neat! Since this is a polyprotic acid, this corresponds to Ka1. Guess what you can determine from the pH at the midpoint of the second titration. This information can be used to help identify the acid in question since Ka for a large number of polyprotic acids are known.

The first acid that you will be following today is citric acid which is an acid that falls into the idealized category. You should see three areas where the pH undergoes significant changes and should be able to determine the three Ka values for citric acid and compare the result to the three known values given below.

            H₃C₆H₅O₇(aq) + H₂O(l) <=> H₂C₆H₇O₇^- + H₃O⁺     K_a1 = 7.4x10^-3 @ 25^oC
               H₂C₆H₅O₇^- + H₂O(l) <=> HC₆H₆O₇^2- + H₃O⁺    K_a2 = 1.7x10^-5 @ 25^oC
               HC₆H₅O₇^2- + H₂O(l) <=> C₆H₅O₇^3- + H₃O⁺       K_a3 = 4.0x10^-7 @ 25^oC

pH Titration Curves 'The Real World':

In reality, many polyprotic acids only show one discernable equivalence point! The vast majority of the time, this corresponds to final equilibrium. If this is the case then, all the other equivalence points can be determined by knowing what type of polyprotic acid one is dealing with, i.e., diprotic or tri protic. For a triprotic acid, the other two equivalence points should correspond to 1/3 and 2/3 of the volume of the base required to reach the final one and thus one can still determine the Ka values. Note, however, I did say the vast majority of the time. How one knows how to determine whether the observed equivalence point equals the removal of the final proton I leave for you to explore! [Hint: what is the pH at the 1/2 equivalence point of a titration of a polyprotic acid equal to]

The second acid that you will be looking at in this lab is phosphoric acid, a triprotic acid whose Ka values are given below.

                 H₃PO₄(aq) + H₂O(l) <=> H₂PO₄^- + H₃O⁺    K_a1 = 7.5x10^-3 @ 25^oC
                    H₂PO₄^- + H₂O(l) <=> HPO₄^2- + H₃O⁺    K_a2= 6.2x10^-8 @ 25^oC
                    HPO₄^2- + H₂O(l) <=> PO₄^3- + H₃O⁺    K_a3= 3.6x10^-13 @ 25^oC

Experimental Procedure:

Your TA will also demonstrate the best set up for this experiment.

Using a graduated cylinder, place ~ 20mL of the ~0.02M citric acid into a small beaker. If necessary add distilled water such that the tip of the pH probe is covered.
Fill your buret with the ~0.02M NaOH solution. Record the exact molarity of this solution. Record the initial buret reading. Remember that this corresponds to 0.00mL of NaOH added.
Record the initial pH of the Citric acid.
Carefully add the NaOH recording the volume of NaOH required to effect a pH change of 0.2. Continue this process until the pH reaches 12.
Plot a graph of 'pH' versus 'Volume of NaOH" added and from this graph determine:

The Ka values for citric acid.
The exact concentration of the citric acid.

Repeat steps one through five using the ~0.02M phosphoric acid and determine the Ka values for phosphoric acid and the exact molarity of the phosphoric acid solution.

Write-up:

In the discussion portion of your write up, be sure to address the correlation between the Ka values that you obtained and those given to you in this procedure. Address any unusual problems that you encountered.